图,现在终于接触到了最短路径,等问题了.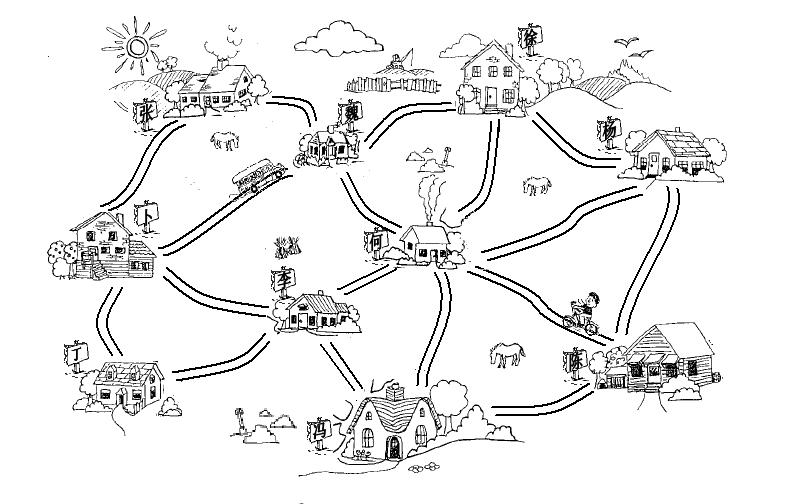
在我们刚刚开始的时候就讲了好几种关系,例如"多对多"
什么是图(Graph)
表示多对多的关系
包含
一组顶点:通常用V(Vertex)表示顶点集合.
一组边:通常用E(Edge)表示边的集合
边时顶点对:(v,w)∈E,其中的v,w∈V
有向边<v,w>表示从v指向wde边(单行线)
不考虑重边和回路
---------------单项边-------
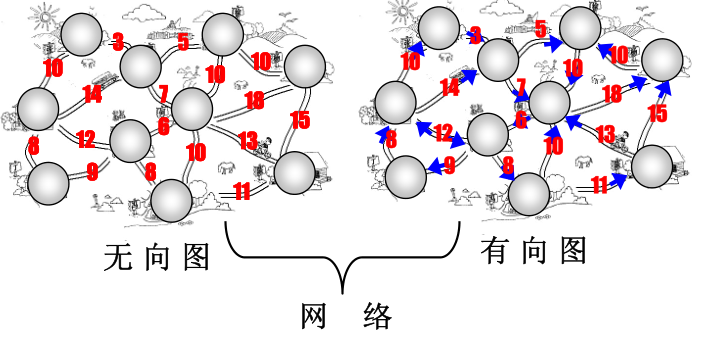
带权重的图我们称之为网络
==========================================================
抽象数据类型定义
类型名称: 图(Graph ) 数据对象集: G(V,E) 由一个非空的有限顶点集合V 和一个有限边集合E 组成。 操作集:图 对于任意图 G Graph及 ,以及 v V, e E Graph Create() :建立并返回空图; Graph InsertVertex(Graph G, Vertex v) :将v 插入G ; Graph InsertEdge(Graph G, Edge e) :将e 插入G ; void DFS(Graph G, Vertex v) :从顶点v 出发深度优先遍历图G ; void BFS(Graph G, Vertex v) :从顶点v 出发宽度优先遍历图G ; void ShortestPath(Graph G, Vertex v, int Dist[]):计算图:计算图G 中顶点v 到任意其他顶点的最短距离; void MST(Graph G) :计算图G 的最小生成树;
-----------------------图在程序中的表示-------------------
首先我们来说第一个:邻接矩阵 用一个二维的数组表示一个图.
-----自己思考一下我们怎样用一个二维数组储存一个图.-----
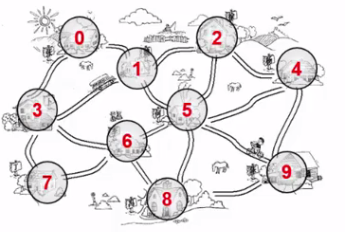

灰常之明显,首先提取出来这个图我们需要储存的数据. 都有什么的村庄的名称(也就是那些编号),和他们之间的连通性.于是我们便可以得出由上图的储存方式.
-------------------然后咱们就可以发现一点有趣的东西,这个二维数组还真不错,有向无向的图都可以储存,哈哈方便-------但是作为一门美到极致的学科,数据结构是不允许,有任何可以避免的浪费的,所以在无向图当中,中间的对角线两边是对称的(具体原因自己想),那么我们能不能节省出来那一部分空间呢?
-----------我想出来的办法是用一位数组来储存上三角的数据,不过在使用的过程中需要计算那个数据是第几行第几列的,可能会造成时间上的浪费------
哈哈,陈越老师当时问完那个学生之后一定很无语..... (不要搞错~~~~)
------汗~~~想的对了~~~~------------------
------------------------猜的实现方式也对了-------------------------猜的问题也对了----------------------------
用一个长度为N(N+1)/2 的1 维数组A 存储{G 00 ,G 10 ,G 11 ,……,G n-1 0 ,…,G n-1 n-1 },则G ij,则G ij 在A 中对应的下标是:( i*(i+1)/2 + j )对于 网络 ,只要把G[i][j] 的值定义为边 的权重即可。
邻接矩阵 —— 有什么好处? 直观、简单、好理解 方便检查任意一对顶点间是否存在边 方便找任一顶点的所有“邻接点”(有边直接相连的顶点) 方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”)方便计算任一顶点的“度”(从该点发出的边数为“出度”,指向该点的边数为“入度”) 无向图:对应行(或列)非0 元素的个数 有向图:对应行非0 元素的个数是“出度”;对应列非0元素的个数是“入度”
邻接矩阵 —— 有什么不好? 间 浪费空间 —— 存稀疏图(点很多而边很少)有大量无效元素 对稠密图(特别是完全图)还是很合算的 浪费时间 —— 统计稀疏图中一共有多少条边
为了避免像邻接矩阵这样,当矩阵为稀疏矩阵式十分浪费时间空间的情况下我们就像到了另一种储存方法-------邻接表----------
邻接表:G(N)为指针数组,对应矩阵每行一个链表,只存非零元素......还是那个小城镇自己想象怎么储存--------思考时间 ---马上会来
-------再次猜中-----汗~~~是不是太简单了?~~~~~~~~~~~~~~~------------------------
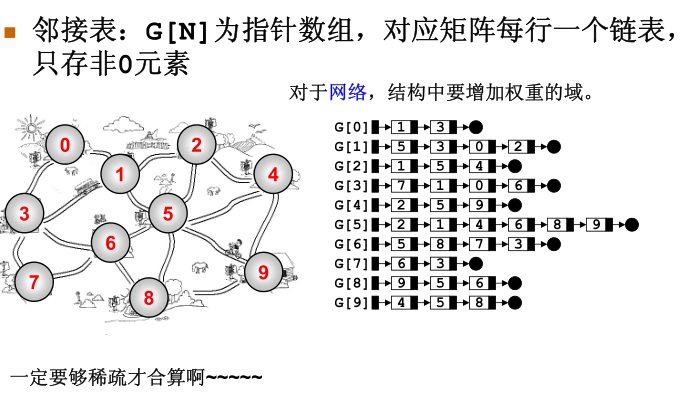
~~~~~~~~~汗~~~~~~~还是小陈姐姐说得对~~~足够稀疏才合算~~~~~~
-----有有问题了---多稀疏才核算------有点太那个啥了吧----好抠----0_0----不想了,,,过过过过---
